Борборго умтулуучу күч

 

 

Жабдуулар:     

               - айлануу платформасы;

-  жүк жана чыгырыктар;

-  фотогейт (Fotogate);

-  смарт таймер (Smart Timer);

-  генератор;

-  суу таразасы;

-  миллиметрдик кагаз;

-  жип

 

Максат:  Айлана боюнча кыймылда болгон нерсенин массасынын жана айлануу радиусунун өзгөрүшүнүн борборго умтулуучу күчкө болгон таасирин изилдөө.

 

Айлана боюнча кыймыл. Ийри сызыктуу кыймылдын эң жөнөкөй түрү болуп нерсенин айлана боюнча бир калыпта кыймылы эсептелет. Бул учурда анын  сызыктуу ылдамдыгы модулу боюнча өзгөрбөйт, ал эми кыймылдын траекториясы  радиустуу айлана болот.

Алга умтулуу кыймылынын кинематикасындагы негизги чоңдуктар: которулуш, сызыктуу ылдамдык, сызыктуу ылдамдануу ж.у.с. бардык эле механикалык кыймылдарды мүнөздөө үчүн жетиштүү эмес. Нерсенин айлана боюнча кыймылын мүнөздөө үчүн дагы кошумча чоңдуктарды киргизүү зарыл. Алар: айлануу мезгили, айлануу жыштыгы, бурулуу бурчу, бурчтук ылдамдык, бурчтук ылдамдануу.

Бир толук айланууга кеткен убакыт айлануу мезгили деп аталып,  тамгасы менен белгиленет жана анын СИ системасындагы бирдиги  (секунда). Айлануу мезгилине тескери пропорциялуу чоңдук айлануу жыштыгы деп аталып,  тамгасы менен белгиленет ().

Бир калыпта айлана боюнча кыймыл (же айлануу кыймылы) учурундагы нерсенин айлануусунун жыштыгы нерсенин 1 секундада жасаган айлануу санына барабар жана анын бирдиги .

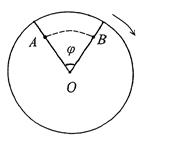
6.1-сүрөт

Айлана боюнча кыймылдаган нерсенин абалынын өзгөрүшүн бурулуу бурчу деп аталган чоңдук менен мүнөздөө бир кыйла ыңгайлуу.

Нерсе кандайдыр  радиустуу айлана боюнча кыймылга келсин (6.1-сүрөт). Айлананын  борборунан нерсенин кандайдыр  чекитинде жайгашкан радиуста бурулганын көрөбүз. Мисалы, эгерде  убакыт аралыгында нерсе  чекитинен  чекитине которулса, анда ушул эле убакытта радиус  бурчуна бурулат. Бул бурч радиустун бурулуу бурчу деп аталат. Бурулуу бурчунун бирдиги катары  (радиан) колдонулат.

Бурулуу бурчунун, ошол бурулуу болуп өткөн убакытка болгон катышы менен ченелүүчү чоңдук бурчтук ылдамдык деп аталат. Аны убакыт бирдигиндеги бурулуу бурчунун чоңдугу деп да алууга болот:

 

(6.1) формула боюнча бурчтук ылдамдыктын бирдиги, бурч радиан менен туюндурулса,  болору көрүнүп турат.

Бурчтук ылдамдыкты  айлануу жыштыгы  же  айлануу мезгили  аркылуу туюнтууга болот:

 

 

 Нерсенин айлана боюнча кыймылы бир калыпта өзгөрмөлүү, тагыраак атканда, бир калыпта ылдамдатылган же акырындатылган болушу мүмкүн.

Эгерде нерсенин бурчтук ылдамдыгы өзгөрмөлүү болсо, бурчтук ылдамдыктын канчалык жай же тез өзгөрүшүн мүнөздөө үчүн бурчтук ылдамдануу деп аталган физикалык чоңдук киргизилет. Бурчтук ылдамдануу бурчтук ылдамдыктын өзгөрүшүнүн, ошол өзгөрүү болуп өткөн убакытка болгон катышы менен аныкталат. Убакыт бирдигиндеги бурчтук ылдамдыктын өзгөрүшүн мүнөздөөчү физикалык чоңдук бурчтук ылдамдануу деп аталат.

Бурчтук ылдамданууну  тамгасы менен белгилеп, айлана боюнча бир калыпта ылдамдатылган же акырындатылган кыймылдар үчүн төмөнкүдөй жаза алабыз:

 

Бурчтук ылдамдануунун бирдиги  же .

Айлануу мезгили жана айлануу жыштыгы аркылуу нерсенин айлана боюнча кыймылы учурундагы сызыктуу ылдамдыгынын модулун оңой эле туюнтуп алууга болот:

 

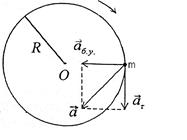
6.2-сүрөт

Нерсенин айлана боюнча бир калыпта кыймылы учурунда сызыктуу ылдамдыгынын модулу өзгөрбөсө да, ылдамдык вектору турактуу эмес, ал багыты боюнча өзгөрүп турат. Мындан бул кыймыл ылдамдатылган кыймыл экендиги келип чыгат. Бул учурдагы сызыктуу ылдамдануу векторунун багыты сызыктуу ылдамдык векторунун багыты менен дал келбейт. Нерсенин  сызыктуу ылдамдыгы траекториянын каалагандай чекитинде айланага жаныма боюнча багытталган, ал эми  ылдамдануу вектору эки түзүүчүгө ажыратылышы мүмкүн:  жана  (6.2-сүрөт). Мында - тангенциалдуу ылдамдануу деп аталуучу  векторунун траекториянын берилген чекитине жаныма боюнча түзүүчүсү; - борборго умтулуучу же нормалдык ылдамдануу деп аталуучу  векторунун траекториянын берилген чекитине жүргүзүлгөн жанымага нормаль (радиус) боюнча түзүүчүсү (=).

Сызыктуу ылдамдыктын сан маанисинин өзгөрүшүнүн тездигин мүнөздөөчү чоңдук тангенциалдуу ылдамдануу деп аталат.

Сызыктуу ылдамдыктын багытынын өзгөрүшүнүн тездигин мүнөздөөчү чоңдук борборго умтулуучу же нормалдык ылдамдануу деп аталат.

Сүрөттөн

 

экендиги көрүнүп турат.

Айлана боюнча бир калыпта кыймыл  учурунда сызыктуу ылдамдыктын сан мааниси өзгөрбөгөндүктө, =0, сызыктуу ылдамдануу борборго умтулуучу ылдамданууга барабар = жана радиус боюнча айлананын борборун көздөй багытталган.

= жана  формулаларын колдонуу менен борборго умтулуучу ылдамдануу үчүн төмөнкү формуланы жаза алабыз:

 

Борборго умтулуучу күч. Нерселердин айлана боюнча кыймылы, чоңдугу боюнча турактуу, ал эми багыты дайыма ылдамдык векторуна перпендикуляр болгон күчтүн таасири менен болот. Бул учурда нерсеге таасир эткен күч борборго умтулуучу күч деп аталат. Борборго умтулуучу күч радиус боюнча айлануу борборуна багытталып, нерсенин айлана боюнча кыймылга келишин камсыз кылат. Бул күч, багыты өзүнүн багыты менен дал келген, борборго умтулуучу ылдамданууну пайда кылат.

Ньютондун II законун жана (6.6) формуласын пайдаланып,  радиустагы айлана боюнча кыймылдаган нерсеге таасир эткен борборго умтулуучу күч төмөнкүчө жазууга болот:

 

Борборго умтулуучу күч - бул күчтүн жаңы түрү эмес, бул нерсени айлана боюнча кыймылдаткан күчтүн аты. Борборго умтулуучу күчтүн табияты ар бир конкреттүү учур үчүн ар түрдүү (сүрүлүү күчү, серпилгич күчү, тартылуу күчү ж.б.у.с.) болушу мүмкүн. Көпчүлүк учурда борборго умтулуучу күч нерсеге таасир эткен бир нече күчтөрдүн натыйжалоочусу же кандайдыр бир күчтүн бир түзүүчүсү болот.